Thanks M+A for looking at my previous sloppy sketches! And M, thanks for your proposed challenge to me: try to represent Quantum Teleportation as a sum-of-paths.
This ate my mind for a week.
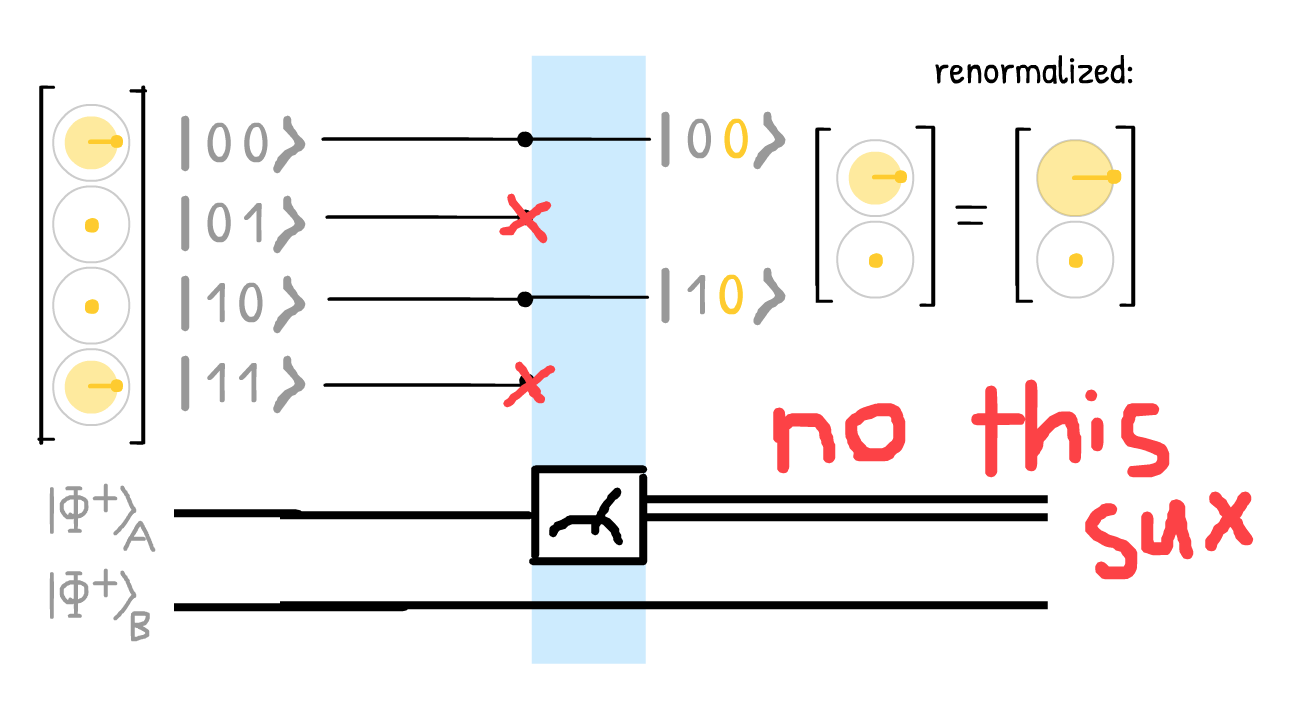
My first attempt went like this. Regular Copenhagen interpretation, assume probabilities "collapse" after a measurement (and are then re-normalized):

In this sketch, the measurement is a "filter" that kills all paths where the Qubit A ≠ 0.
I did not like this. If the circuit had N measurements, I'd have to show 2^N different graphs, one for each possibility of measurements. You wouldn't be able to see the whole system at once.
After thinking about it more, I realized there was an easy but... uh... maybe philosophically awkward way to make a more compact visualization.
Just add parallel universes.
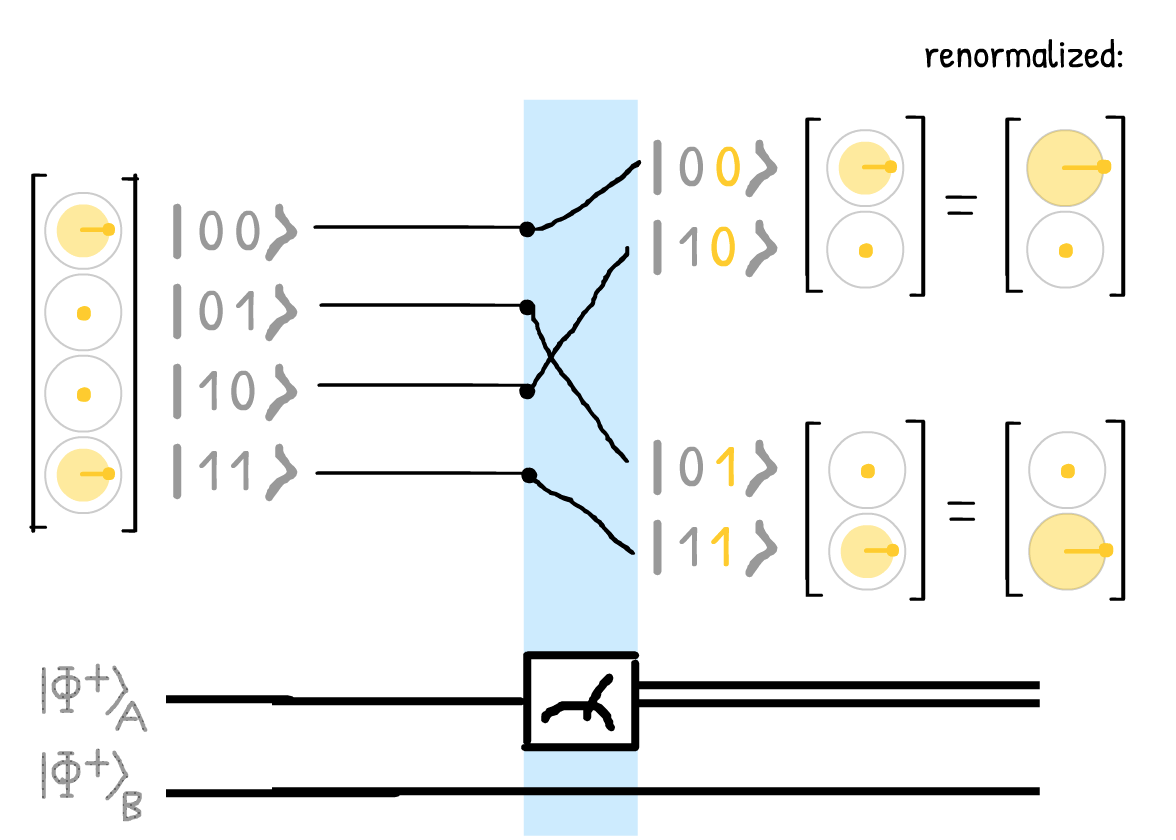
(IMPORTANT NOTE: this visualization does NOT assume or assert Many Worlds Interpretation, any more than a flowchart diagram would. But gosh dang, Many Worlds sure makes for a convenient visualization!)
In this sketch, the measurement is a "sorter" that separates paths where Qubit A is 0 or 1. After the measurement, paths in one "fork" can never interact with paths in the other.
Paths aren't removed, they're just moved. Now you can see all measurement possibilities at once!
And to show a CNOT conditional on a measurement, just apply the NOT-gate only to the fork where the measurement = 1!
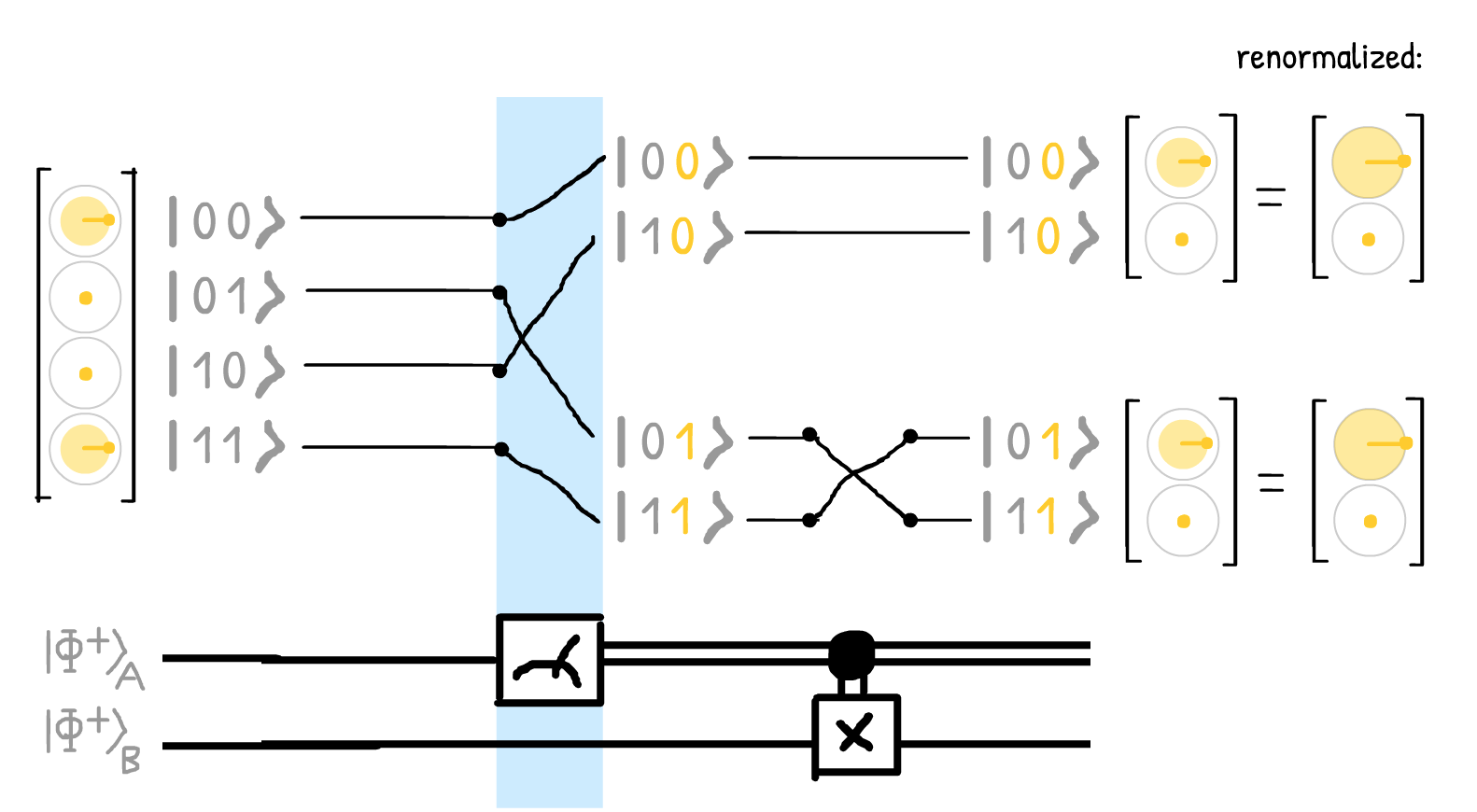
With this visual grammar laid out, we can finally show the good ol' Quantum Teleportation circuit as a sum-of-paths! Voilà:

(Note: all amplitudes are scaled by 1/√2 as they pass through the Hadamard gate. Orange arrows represent an amplitude getting π-phase-flipped)
Hm... it's a bit messy in the beginning. Is there a way to simplify it?
Yes! Remember our input vector is the tensor product of |ψ〉(the qubit we wanna teleport) and |ϕ+〉(our two entangled qubits). So our input vector is:

The middle four amplitudes are zero – therefore, they can't affect the sums-of-paths! So, let's eliminate all the paths that start from any of those amplitudes:
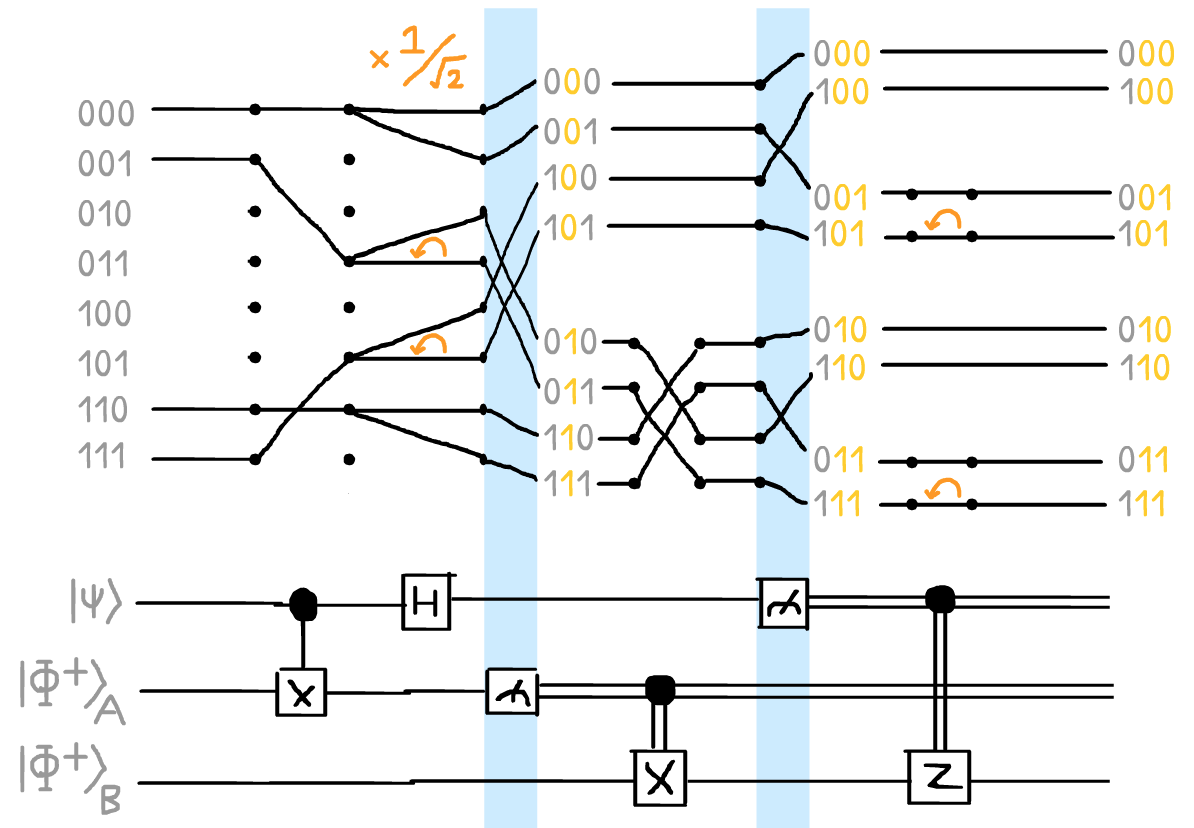
And now, if you follow the paths backwards, you can see that every output amplitude comes from one and only one input amplitude! For example:
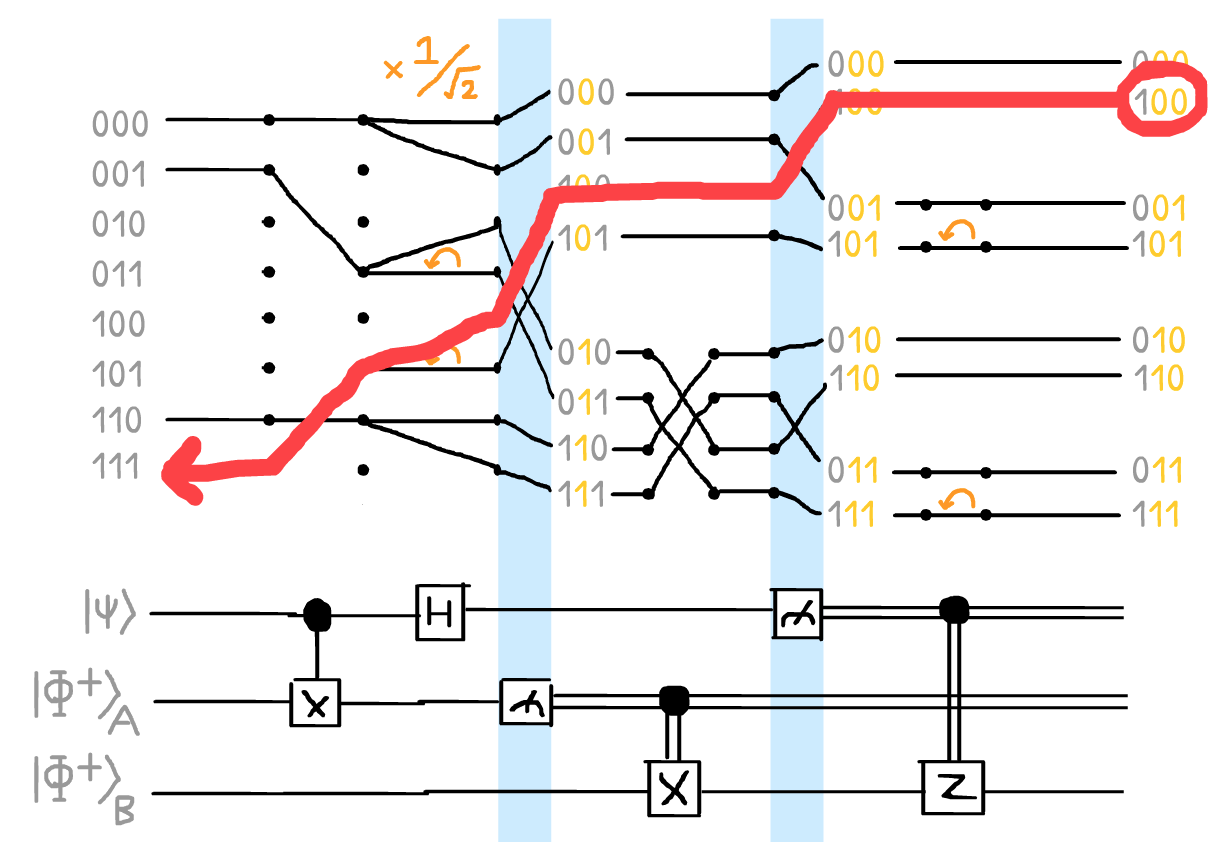
(Also note: every path that goes through a π-phase-flip does so twice. Meaning, all phase-flips are undone, every amplitude retains its original phase.)
So, if we plug our tensor product as the input, then follow each path backwards from the output, we can calculate the sum-of-paths for each output amplitude, renormalize...
...and PROVE that the Quantum Teleportation circuit, does, indeed, teleport any arbitrary quantum state!
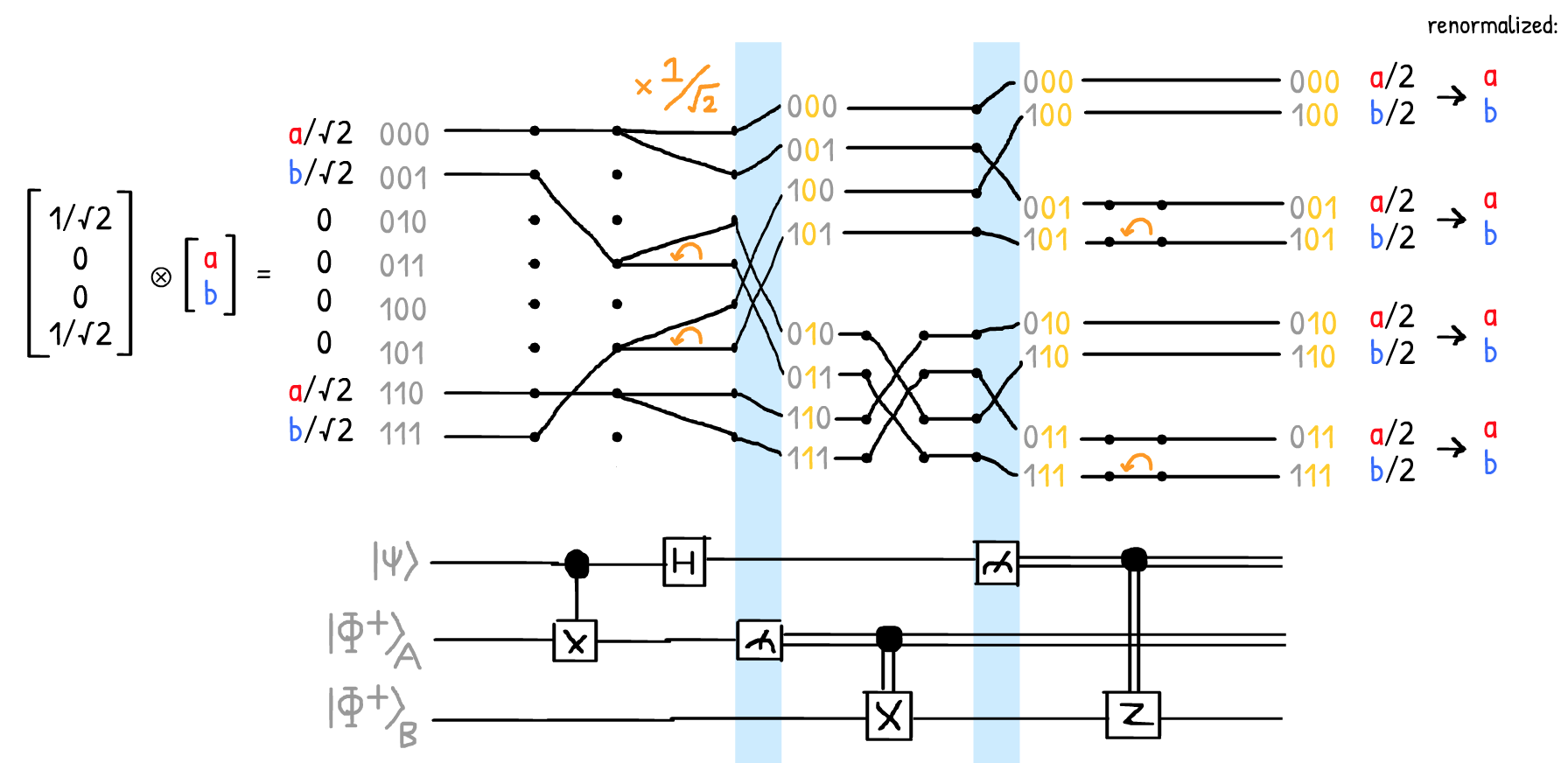
(Theoretically, I should re-normalize after each measurement, but since re-normalization scales all amplitudes in a fork by the same constant, and amplitudes in one fork can't interact with those in another, it's fine to just re-normalize at the end)
I dunno if I'm crazy... but it seems this sum-of-paths method almost makes it trivial to prove the Quantum Teleportation circuit! Just follow the yellow brick road paths backwards!
What do you think, A+M? Was this a useful way of seeing/proving Quantum Teleportation? How did this compare to other explanations of the QT circuit? What was unclear – or wrong – in my first-draft visualization/explanation?
Many thanks again!
P.S: One thing I don't get. The third qubit only has two gates acting on it: an X gate, which doesn't rotate phases, and a Z gate, which rotates a phase exactly by π. And yet, we can teleport a state with any arbitrary phase, like π/4, even though there's no way to get π/4 from X swaps and Z π-phase-flips. I... what? How? That's some spooky action.