Un movimiento pacifico lucha contra la violencia y opresión por años, pero nada cambia mucho. Luego, de repente, todo cambia.
¿Por qué tantos sistemas complejos – culturas, el medio ambiente, la economía – parecen atascados (o en el mejor de los casos, "estables") a pesar de todo el esfuerzo para cambiarlos? ¿Y por qué, cuando el cambio eventualmente llega, parece afectar (o en el peor de los casos, "colapsar") todo al mismo tiempo?
Existe una herramienta que nos puede ayudar a entender esto:
los campos de atractores. ![]() O, en palabras menos sofisticadas: "una pelota cayendo desde unas montañas".
Esta herramienta fue creada originalmente en el campo de la física,
pero ahora se usa para entender la genética, la neurociencia, las alianzas políticas, y más!
O, en palabras menos sofisticadas: "una pelota cayendo desde unas montañas".
Esta herramienta fue creada originalmente en el campo de la física,
pero ahora se usa para entender la genética, la neurociencia, las alianzas políticas, y más!
Voy a explicar los atractores con un ejemplo del medio ambiente. Imagina que estas pescando en una pequeña laguna. Puedes agotar la población de peces fácilmente...
Por suerte, los peces se reproducen, así que tu población de peces vuelve a crecer con el tiempo. Por desgracia, por encima de un punto, los peces se mueren por sobrepoblación. Y por aun mas desgracia, por debajo de un punto, no quedan suficientes peces para reproducirse.
Ahora, vamos a pescar, con estas fuerzas de la vida y la muerte:
Si no pescas demasiado, el ecosistema se mantiene "atraído" a Población=70. ¡Felicitaciones, eres sustentable! Pero si pescas mucho, el ecosistema es "atraído" a Población=0. ¡Has matado a todos!
Nada cambia mucho. Hasta que de repente, todo cambia.
Por estas razones Población=0 y Población=70 son llamados atractores: porque "atraen" el sistema a esos puntos. De la misma manera, Población=30 es llamado un repelente, porque si la población esta un poco por encima o debajo de 30, es "repelida" lejos de 30. Población=30 es también llamado un punto de inflexión porque ahí es donde el ecosistema cambia del atractor de Población=70 al de Población=0
Uf, esas son muchas palabras complicadas.
¿No estaría bueno directamente poder ver como el sistema funciona en todas las poblaciones?
¡Aquí es donde los campos de atractores nos pueden ayudar!
Si convertimos el cambio de población ![]() en una serie de montañas
en una serie de montañas ![]() (mas cambio → montañas mas empinadas)
y ponemos una pelota
(mas cambio → montañas mas empinadas)
y ponemos una pelota ![]() en la montaña,
conseguimos algo como esto:
en la montaña,
conseguimos algo como esto:
¡Ahora, dibujado como un campo de atractores, ver lo que esta pasando es mucho mas fácil!
Las montañas ![]() son repelentes;
Los valles
son repelentes;
Los valles ![]() son atractores.
son atractores.
La profundidad de un valle representa cuanta energía se necesita para salir del atractor. (por ej.: Población=0 es mas profundo que Población=70; por eso es mas fácil colapsar el ecosistema que arreglarlo.)
El ancho de un valle es llamado la cuenca de atracción – el rango en el que el atractor atrae, valga la redundancia. (por ej.: la cuenca de atracción de Población=70 esta adentro del rango 30<Población≤100)
(Nota: nuestro campo de atractores es 2D, porque solo tenemos un parámetro: la población. Si tuviéramos mas parámetros, podríamos tener un campo 3D, 4D, 5D, ¡O incluso 100D! Y en dimensiones mas altas, puedes conseguir lo que se llama atractores extraños... pero eso es para otro día.)
En nuestra metáfora de la pelota y las montañas, pescar y liberar peces es equivalente a empujar la pelota. ¿Pero que tal si pudieras mover las montañas? En este ejemplo de la pesca, eso significaría cambiar los atractores del sistema, mediante la introducción de depredadores, el aumento de la vegetación, etc.
Si solo intentas empujar la pelota, esta podría volver al atractor. ¡Pero si mueves las montañas, tus cambios se van a mantener! Estas cambiando el sistema en sí.
Veamos algunos ejemplos no relacionados con la pesca, para demostrar que los campos de atractores son una herramienta poderosa para entender sistemas. Aquí hay algunos ejemplos de papeles académicos (se puede notar que son de academia, ya que sus diagramas se parecen a presentaciones de Powerpoint):
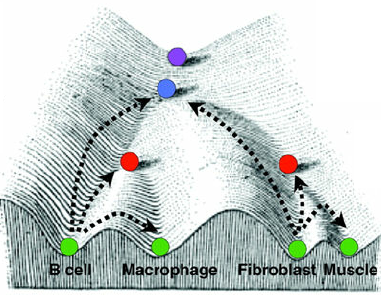 epigenética: como las células madre se transforman en células especializadas
(fuente)
epigenética: como las células madre se transforman en células especializadas
(fuente)
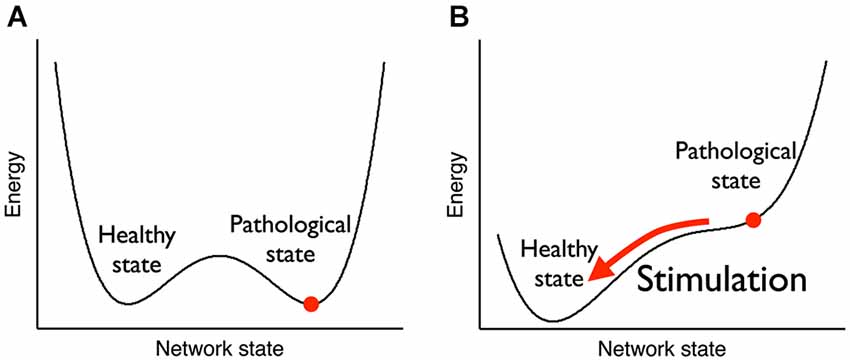 neurociencia: la estimulación neurológica lleva tu cerebro desde un estado poco sano estable a un estado sano estable.
(fuente)
neurociencia: la estimulación neurológica lleva tu cerebro desde un estado poco sano estable a un estado sano estable.
(fuente)
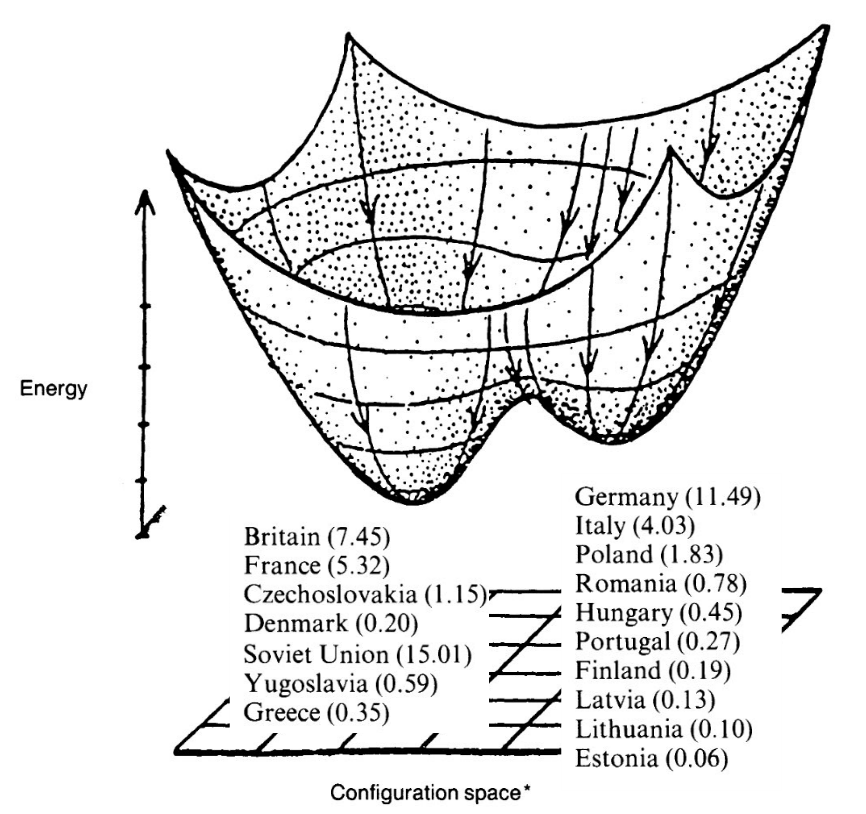 ciencia política: "predecir" probables alineamientos políticos durante la segunda guerra mundial
(fuente)
ciencia política: "predecir" probables alineamientos políticos durante la segunda guerra mundial
(fuente)
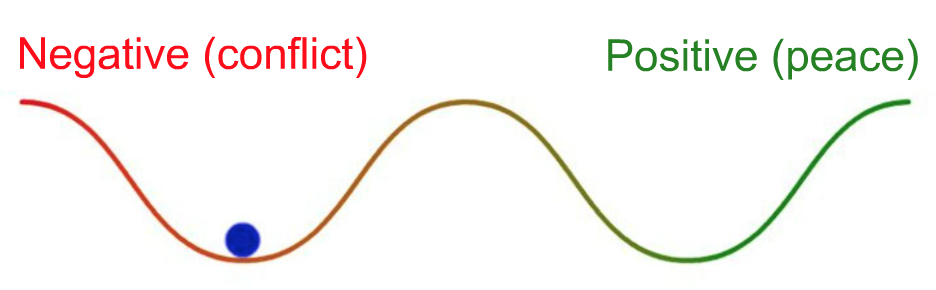 estudios de paz: la paz no es la ausencia de la guerra – ¡son diferentes atractores!
(fuente)
estudios de paz: la paz no es la ausencia de la guerra – ¡son diferentes atractores!
(fuente)
Finalmente, veamos la simulación de pesca con nuestros nuevos conocimientos
Así que, la próxima vez que te preguntes porque las cosas están atascadas de cierta manera, piensa:
- ¿Cuáles son los "atractores" del sistema?
- ¿Qué tan "profundos" son los valles? (mas profundo = mas difícil de salir)
- ¿Qué tan "anchos" son los valles? (mas ancho = mayor rango de atracción)
- Además de mover la pelota, ¿podemos mover las montañas? (cambiar el sistema)
Y si en algún momento te sientes frustrado por el mundo, recuerda: para muchos sistemas, por largos periodos de tiempo, nada cambia.
Hasta que de repente, todo cambia.