Un mouvement pacifiste se bat contre la violence et l'oppression pendant des années, et rien de change vraiment. Puis, tout se met à changer.
Pourquoi est-ce que beaucoup de systèmes complexes (cultures, environnements, économies) semblent coincés (ou "stables") malgré beaucoup d'efforts pour les changer ? Et pourquoi, quand le changement arrive, tout semble s'enchaîner en même temps ?
Il existe un outil qui peut nous aider à comprendre cela:
les paysages attracteurs. ![]() Ou, dans des termes moins pompeux, "une balle dévalant des collines".
Cet outil a été initialement créé en physique,
mais a depuis été utilisé pour nous aider à comprendre la génétique, la neuroscience, les alliances politiques, et bien plus !
Ou, dans des termes moins pompeux, "une balle dévalant des collines".
Cet outil a été initialement créé en physique,
mais a depuis été utilisé pour nous aider à comprendre la génétique, la neuroscience, les alliances politiques, et bien plus !
Je vais vous expliquer les attracteurs en utilisant un exemple environnemental. Disons que vous pêchez sur un petit (et minable) étang. Vous pouvez épuiser vos ressources naturelles en poisson assez facilement...
Heureusement, les poissons se reproduisent, donc la population de poissons augmente avec le temps. Malheureusement, au-delà d'un certain seuil, les poissons meurent de surpopulation. Et malheureusement bis, en-deçà d'un certain seuil, les poissons sont trop peu nombreux pour se reproduire plus vite qu'ils ne meurent.
Maintenant, pêchons avec ces forces de croissance et de mort :
Si vous n'attrapez pas trop de poissons, l'écosystème reste "attiré" à Population=70. C'est viable ! Cependant, attrapez-en trop, et l'écosystème est "attiré" à Population=0. Vous les avez tous tués !
Rien ne change vraiment. Puis, tout se met à changer.
C'est pour cela que Population=0 et Population=70 sont appelés des attracteurs : parce qu'ils "attirent" le système à eux. De la même manière, Population=30 est appelé un répulseur, étant donné que si la population est un peu en dessous ou au-dessus de 30, elle est "repoussée" de cette valeur. Population=30 est aussi appelé un point de basculement car c'est là que l'écosystème "bascule" de l'attracteur Population=70 à l'attracteur Population=0.
Pfiou, ça fait beaucoup de mots.
Ne serait-ce pas sympa de simplement voir comment le système de comporte à tous les nombres possibles pour la population ?
C'est là que les paysages attracteurs nous viennent en aide !
Si nous convertissons la vitesse de croissance/mort ![]() en une série de pentes
en une série de pentes ![]() (grandes vitesses → pentes raides) et mettons une balle
(grandes vitesses → pentes raides) et mettons une balle ![]() dessus,
nous obtenons quelque chose comme ça :
dessus,
nous obtenons quelque chose comme ça :
Maintenant que le système est dessiné comme un paysage, voir ce qu'il fait est facile !
Les sommets ![]() sont les répulseurs;
Les vallées
sont les répulseurs;
Les vallées ![]() sont les attracteurs.
sont les attracteurs.
La profondeur d'une vallée est la quantité d'énergie qu'il faut pour échapper à l'attracteur. (Par exemple, Population=0 est plus profond que Population=70, c'est pourquoi il est plus facile de détruire un écosystème que de le restaurer.)
La largeur d'une vallée est appelée le bassin d'attraction, l'intervalle dans lequel l'attracteur attire. (Par exemple, le bassin d'attraction de Population=70 est toute population avec 30<Population≤100)
(N.B. : notre paysage attracteur est en 2D, car nous n'avons qu'un seul paramètre : la population. Si nous avions eu plus de paramètres, nous aurions pu avoir un paysage en 3D, voire en 4D, en 5D, ou en 100D ! Et à des dimensions plus élevées, on peut même obtenir ce qui est appelé un attracteur étrange... mais ce sera pour une autre fois.)
Dans notre métaphore balle-et-colline, attraper et relâcher des poissons correspond à essayer de déplacer la balle. Et si vous pouviez déplacer les collines ? Dans cet exemple de pêche, cela signifierait changer les attracteurs de l'écosystème, en ré-introduisant des prédateurs, augmentant la vie végétale, etc.
Si vous pouviez juste déplacer la balle, elle pourrait ne faire que revenir à l'attracteur. Mais si vous déplacez les collines, vos changements persévéreront ! Vous modifiez le système sous-jacent lui-même.
Regardons quelques exemples ne concernant pas la pêche, pour vous montrer à quel point les paysages attractifs sont une manière vraiment puissante de comprendre les systèmes. En voici quelques uns issus de vrais papiers académiques (ça se voit qu'ils sont académiques, avec leur aspect Powepoint-esque) :
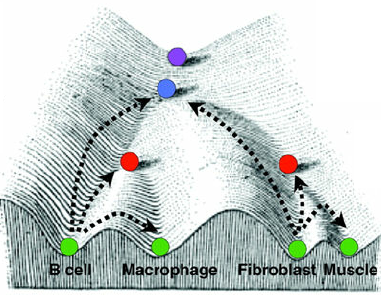 épigénétique : comment les cellules-souches deviennent des cellules spécialisées.
(source)
épigénétique : comment les cellules-souches deviennent des cellules spécialisées.
(source)
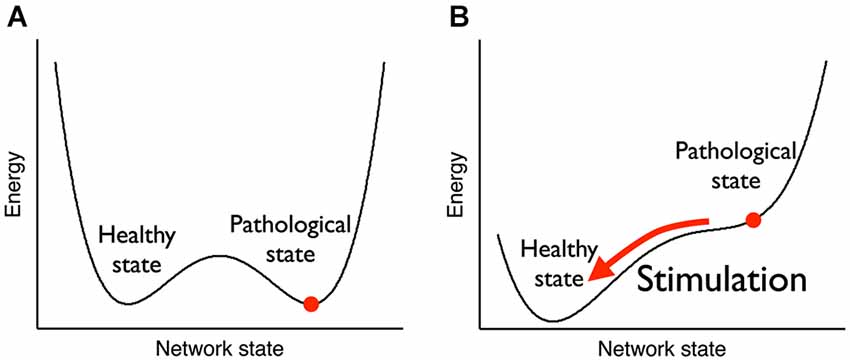 neurosciences : une stimulation neurologique amène votre cerveau depuis un état stable maladif vers un état stable sain.
(source)
neurosciences : une stimulation neurologique amène votre cerveau depuis un état stable maladif vers un état stable sain.
(source)
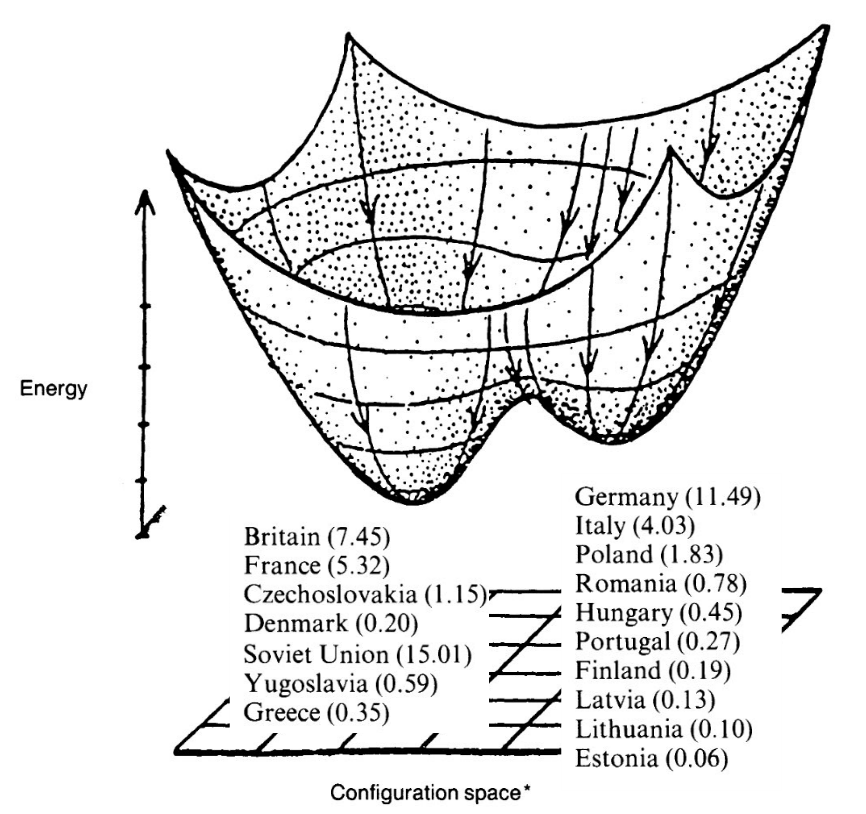 sciences politiques : "prédictions" des alignements politiques probables pendant la Seconde Guerre Mondiale
(source)
sciences politiques : "prédictions" des alignements politiques probables pendant la Seconde Guerre Mondiale
(source)
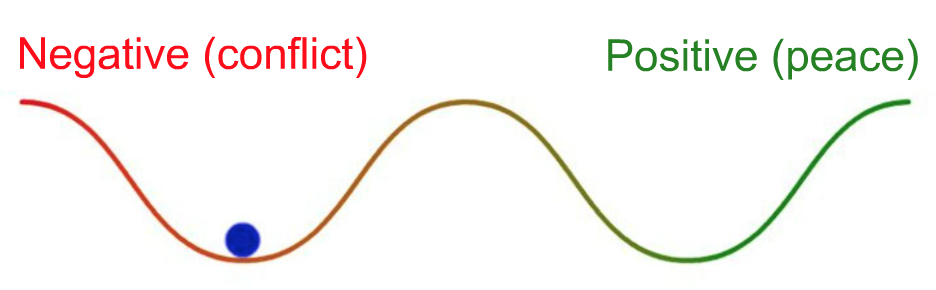 études sur paix : la paix n'est pas la simple absence de guerre : ce sont des attracteurs différents !
(source)
études sur paix : la paix n'est pas la simple absence de guerre : ce sont des attracteurs différents !
(source)
Pour finir, regardons à nouveau notre simulateur de pêche avec tout à la fois !
Donc, la prochaine fois que vous vous demandez pourquoi les choses sont bloquées d'une certaine manière, demandez-vous :
- Que sont les "attracteurs" d'un système ?
- Quelle est la "profondeur" des vallées ? (plus elles sont profondes, plus il est dur d'en sortir)
- Quelle est la "largeur" des vallées ? (plus elles sont larges, plus leur rayon d'attraction est grand)
- Pouvons-nous, en plus de déplacer la balle, déplacer les collines ? (changer le système sous-jacent)
Et si vous vous retrouvez un jour frustré par le monde, souvenez-vous : pour beaucoup de systèmes, pendant de longues périodes, rien ne change vraiment.
Puis, tout se met à changer.