Un movimiento pacífico lucha contra la violencia y la opresión durante años, sin embargo, las cosas no cambian mucho. Entonces, todo cambia.
¿Por qué muchos sistemas complejos - culturas, ambientes, economías – están estancados (o si son buenos, "estables") a pesar de los esfuerzos para cambiarlos? Y ¿por qué, cuando el cambio de hecho llega, parece ajustarse (o si es malo, "colapsa") todo al mismo tiempo?
Hay una herramienta que nos puede ayudar a entender esto:
escenarios atractores ![]() O, en palabras menos rimbombantes: "una pelota rodando en algunas colinas".
Esta herramienta fue creada primeramete en física,
pero desde entonces sea ha usado para ayudarnos a entender genética, neurociencia, alianzas políticas ¡y muchas cosas más!
O, en palabras menos rimbombantes: "una pelota rodando en algunas colinas".
Esta herramienta fue creada primeramete en física,
pero desde entonces sea ha usado para ayudarnos a entender genética, neurociencia, alianzas políticas ¡y muchas cosas más!
A continuación explicaré qué son los atractores con un ejemplo ambiental. Digamos que estás pescando en un estanque pequeñito. Fácilmente puedes agotar los recursos naturales de peces...
Afortunadamente, los peces se reproducen, así que tu poblacion de peces se recupera con el tiempo. Desafortunadamente, arriba de cierto umbral, los peces mueren por sobrepoblación. Y, doblemente desafortunado, debajo de cierto umbral, los peces son demasiado escasos para reproducirse más rápido de lo que mueren.
Ahora, vamos a pescar con estas fuerzas de crecimiento & muerte:
Si no attrapas demasiados peces, el ecosistema permanece "atraído" a Población=70. ¡Eres sustentable! Sin embargo, pesca demasiados y el ecosistema es "atraído" a Población=0. ¡Los mataste a todos!
Casi nada cambia. Entonces, todo cambia.
Por esto, los puntos Población=0 y Población=70 son llamados atractores: ya que "atraen" el sistema a ellos. De la misma forma, Población=30 es llamado un repelete, porque si la población está ligeramente arriba o abajo de 30, es repelida lejos de 30. Población=30 es también llamado un punto de inflexión porque ahí es donde el ecosistema "se flexiona" desde el atractor Población=70 hacia el atractor Población=0.
Uff, esas son muchas palabras.
¿No sería más sencillo ver cómo el sistema se comporta en todos los posibles tamaños de población?
¡Es ahí donde los escenarios de atractores nos ayudan!
Si convertimos la velocidad de crecimiento/muerte ![]() en una serie de laderas de colinas
en una serie de laderas de colinas ![]() (velocidades más rápidas → laderas más inclinadas) y ponemos una pelota
(velocidades más rápidas → laderas más inclinadas) y ponemos una pelota ![]() on top,
obtenemos algo como esto:
on top,
obtenemos algo como esto:
Ahora, cuando dibujamos esto como un paisaje, ¡ver lo que pasa es muy fácil!
Las Colinas ![]() son repelentes;
Los Valles
son repelentes;
Los Valles ![]() son atractores.
son atractores.
La profundidad del valle representa cuánta energía se necesita para escapar del atractor. (por ejemplo: el punto Población=0 es más profundo que Población=70; es por eso que es más fácil colapsar un ecosistema que restaurarlo.)
El ancho de un valle es llamado cuenca de atracción – el alcance dentro del cual el atractor, pues, atrae. (por ejemplo: la cuenca de atracción de Población=70 se extiende entre 30<Población≤100)
(Nota: nuestro escenario de atracción es 2D, porque sólo tenemos un parámetro: Población. Si tuviéramos más parámetros, podríamos tener un escenario 3D, o incluso 4D, 5D, ¡o 100D! Y en dimensiones superiores, puedes incluso tener lo que se conoce como atractores extraños... pero eso es para otro día.)
En nuestra metáfora de la bola y la colina, tú tratas de mover la pelota atrapando & liberando peces. ¿Pero qué pasaría si tú mueves las colinas? En este ejemplo de pesca, eso significaría cambiar los atractores del ecosistema, al reintroducir depredadores, incrementar la vida vegetal, etc.
Si sólo mueves la pelota, ésta sólo volverá a un atractor. Pero si mueves las colinas, ¡tus cambios se quedarán! Estás cambiando el sistema en sí mismo.
Ahora veamos algunos ejemplos que no tengan que ver con pesca, para mostrar cómo los escenarios atractores son métodos poderosps para entender sistemas complejos. Aquí hay algunos de artículos científicos reales (puedes notar que vienen de la academia, por esa apariencia tan de diapositiva):
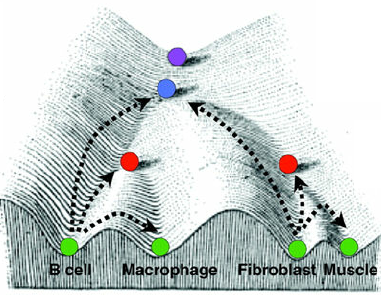 epigenética: cómo las células madre se convierten en células especializadas
(fuente)
epigenética: cómo las células madre se convierten en células especializadas
(fuente)
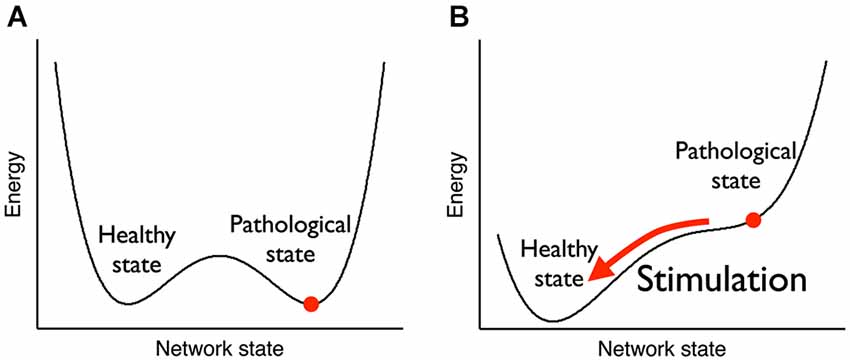 neurociencia: simulación neurológica lleva a tu cerebro de un estado enfermo e inestable a uno saludable y estable.
(fuente)
neurociencia: simulación neurológica lleva a tu cerebro de un estado enfermo e inestable a uno saludable y estable.
(fuente)
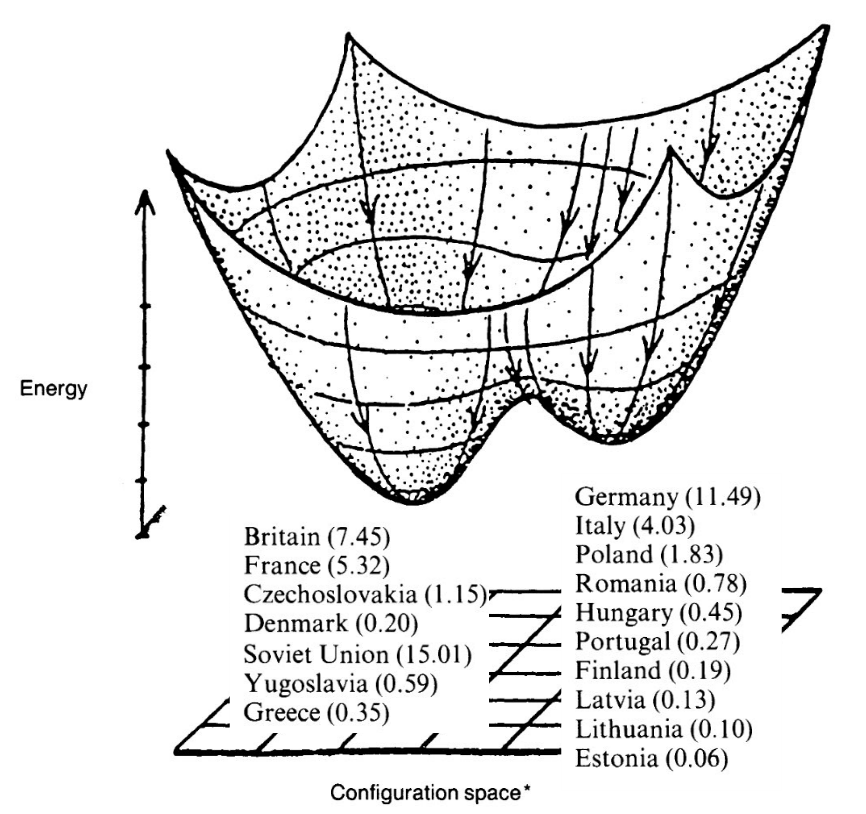 ciencias políticas: "predicción" de alineamientos políticos durante la Segunda Guerra Mundial.
(fuente)
ciencias políticas: "predicción" de alineamientos políticos durante la Segunda Guerra Mundial.
(fuente)
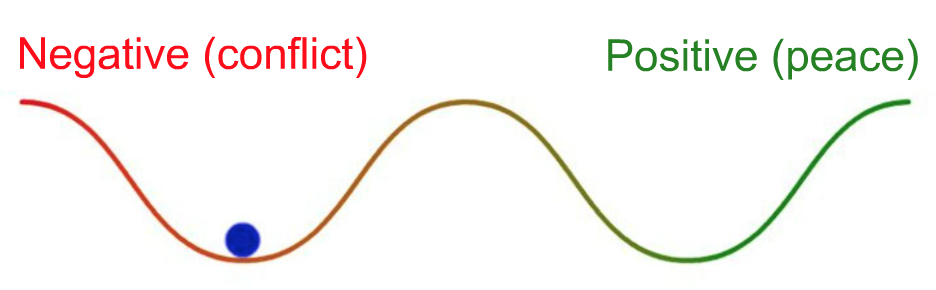 estudios de paz: paz no es la mera auscencia de guerra – ¡son atractores distintos!
(fuente)
estudios de paz: paz no es la mera auscencia de guerra – ¡son atractores distintos!
(fuente)
Finalmente, veamos nuestra simulación de pesca una vez más, ¡ahora con todo al mismo tiempo!
Entonces, la próxima vez que te preguntes por qué las cosas están estancadas en cierta forma, piensa:
- ¿Cuáles son los "atractors" en este sistema?
- ¿Qué tan "profundos" son los valles? (más profundos = más difícil es escapar)
- ¿Qué tan "anchos" son los valles? (más anchos = mayor alcance de atracción)
- ¿Podemos no solamente mover la pelota, sino también mover las colinas? (cambiando el sistema subyacente)
Y si alguna vez te encuentras frustrado con el mundo, recuerda: en muchos sistemas, por largos períodos de tiempo, casi nada cambia.
Entonces, todo cambia.