Rauhanliike taistelee väkivaltaa ja sortoa vastaan vuosia, eikä mikään juuri muutu. Sitten, kaikki muuttuu kerralla.
Miksi monet kompleksiset järjestelmät – kulttuurit, ympäristöt, taloudet – näyttävät olevan jumissa (tai hyvässä tapauksessa "vakaita"), huolimatta ponnisteluista niiden muuttamiseksi? Miksi muutos tapahtuessaan tulee nopeana ryöppynä (tai huonossa tapauksessa romahduksena)?
Tätä voidaan ymmärtää
attraktorimaastojen ![]() tai yksinkertaisemmin “mäkeä alas vierivän pallon”, avulla.
Tämä työkalu luotiin alunperin fysiikan tutkimusalueella, mutta sitä on sittemmin käytetty genetiikassa, neurotieteissä, valtiotieteissä ja monella muulla alalla!
tai yksinkertaisemmin “mäkeä alas vierivän pallon”, avulla.
Tämä työkalu luotiin alunperin fysiikan tutkimusalueella, mutta sitä on sittemmin käytetty genetiikassa, neurotieteissä, valtiotieteissä ja monella muulla alalla!
Selitän attraktoreja tässä ympäristöä koskevan esimerkin avulla. Oletetaan, että kalastat pienellä, surkealla lammikolla. Kalat voivat loppua lammikosta varsin helposti…
Kalat onneksi lisääntyvät, eli populaatio kasvaa ajan myötä suuremmaksi. Valitettavasti jossain vaiheessa ympäristön kantokyky kuitenkin ylittyy, jonka jälkeen kalat kuolevat, koska populaatio on kasvanut liikaa. Vielä valitettavampaa on, että populaatio voi kutistua myös liian pieneksi, jolloin se ei pysty enää lisääntymään riittävästi ja populaatio katoaa.
Mennäänpä kalastamaan näiden kasvun ja kuoleman voimien kanssa:
Jos et kalasta liikaa, ekosysteemi pysyy attraktoituneena populaation kokoon 70. Toimit kestävällä tavalla! Jos kuitenkin kalastat liikaa, ekosysteemi hakeutuu nollaan. Olet tappanut kaikki kalat!
Juuri mikään ei muutu. Sitten kaikki muuttuu.
Tässä esimerkissä populaation kokoja 0 tai 70 kutsutaan attraktoreiksi (attractor), koska ne “vetävät” järjestelmää itseään kohti. Populaation kokoa 30 taas voi kutsua karkottajaksi (repeller), koska populaatio vähän yli tai alle 30 "karkottuu" siitä poispäin. Populaatiota 30 kutsutaan myös keikahduspisteeksi, koska sen kohdalla ekosysteemi "keikahtaa" attraktorista 70 attraktoriin 0.
Oho, paljon sanoja.
Eikö olisi mukavampaa vain katsoa, kuinka järjestelmä käyttäytyy erilaisilla populaatioiden koilla?
Silloin attraktorimaasto auttaa!
Jos muunnamme kasvun/kuoleman nopeuden ![]() sarjaksi rinteitä
sarjaksi rinteitä ![]() (nopeampi vauhti → jyrkemmät rinteet) ja laitamme pallon
(nopeampi vauhti → jyrkemmät rinteet) ja laitamme pallon ![]() mäen päälle, päädymme johonkin tällaiseen:
mäen päälle, päädymme johonkin tällaiseen:
Nyt kun piirretään maisema, on helppo nähdä, mitä järjestelmä tekee!
Kukkulat ![]() ovat karkottajia;
laaksot
ovat karkottajia;
laaksot ![]() ovat attraktoreita..
ovat attraktoreita..
Laakson syvyys kertoo, kuinka paljon energiaa tarvitaan attraktorista pakenemiseksi (esim. kannan koko 0 on syvempi tila, kuin koko 70; siksi ekosysteemi on helpompi romahduttaa, kuin se on elvyttää).
Laakson leveyttä kutsutaan attraktorialtaaksi – alueeksi, jonka sisällä attraktori vetää puoleensa (esim. populaation 70 vetovoima-alue on mikä tahansa kohta alueella 30<Populaatio≤100).
(Huomaa, että attraktorimaisemamme on 2D, koska käytössä on vain yksi parametri: populaation koko. Jos meillä olisi enemmän parametrejä, maisema voisi olla 3D tai jopa 4D, 5D tai 100D! Korkeammissa ulottuvuuksissa saattaa esiintyä myös outoja attraktoreja... mutta jätetään se toiselle päivälle.)
Pallo ja mäki -vertauskuvassamme kalan pyydystäminen ja vapauttaminen tarkoittaa, että siirrät palloa. Entäs jos voisitkin siirtää kukkuloita? Tässä kalastusesimerkissä se tarkoittaisi ekosysteemin attraktorien muuttamista tuomalla lampeen petoeläimiä, lisäämällä kasveja jne.
Jos vain liikutat palloa, se saattaa vain palata attraktorin luo. Mutta jos siirrät kukkuloita, muutokset pysyvät! Muutat taustalla olevaa järjestelmää.
Katsotaanpa joitain muitakin esimerkkejä siitä, kuinka attraktorimaisema on todella hyvä tapa ymmärtää järjestelmiä. Tässä muutamia esimerkkejä tieteellisestä tutkimuksesta (huomaat niiden olevan akateemisista lähteistä, koska ne näyttävät Powerpointilla tehdyiltä):
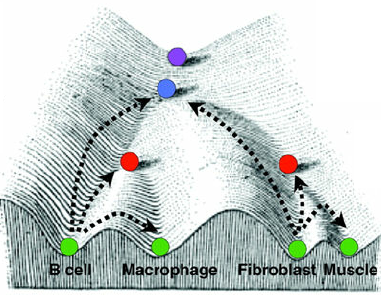 epigenetiikka: miten kantasolut muuttuvat erilaistuneiksi soluiksi.
(lähde)
epigenetiikka: miten kantasolut muuttuvat erilaistuneiksi soluiksi.
(lähde)
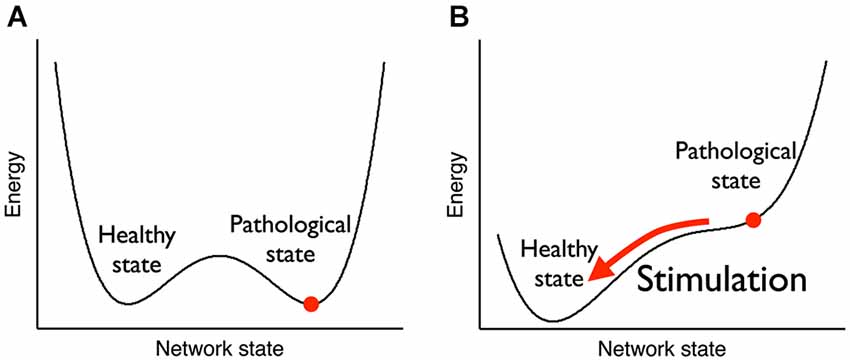 neurotiede: neurologinen simulaatio saa aivot vakaasta epäterveestä tilasta vakaaseen terveeseen tilaan
(lähde)
neurotiede: neurologinen simulaatio saa aivot vakaasta epäterveestä tilasta vakaaseen terveeseen tilaan
(lähde)
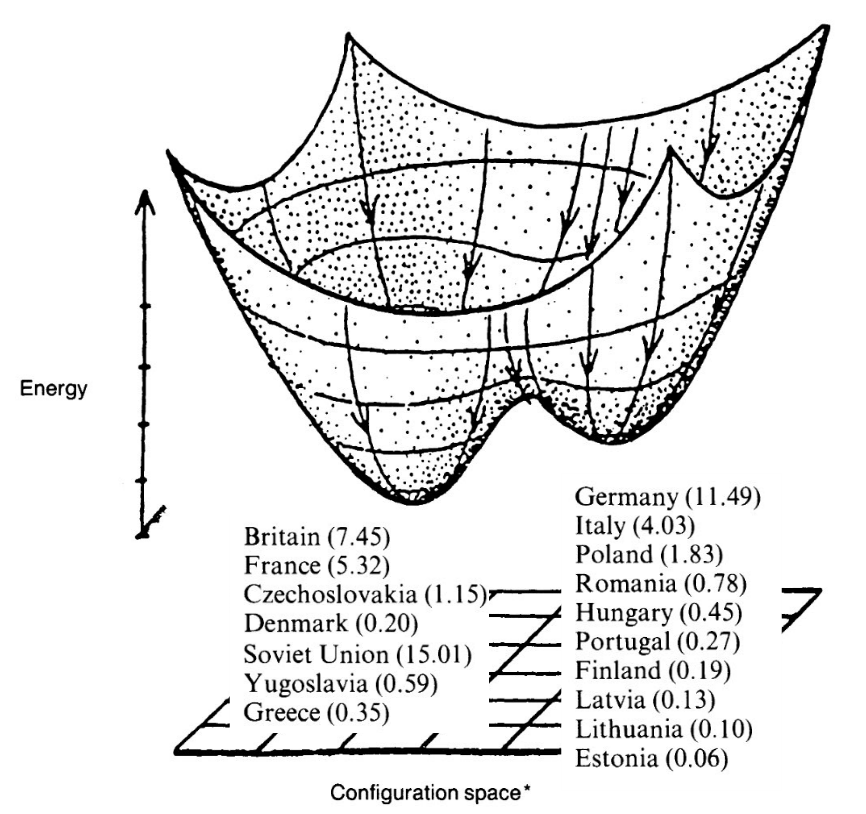 valtiotiede: poliittisen suuntautumisen “ennustaminen” toisen maailmansodan aikana
(lähde)
valtiotiede: poliittisen suuntautumisen “ennustaminen” toisen maailmansodan aikana
(lähde)
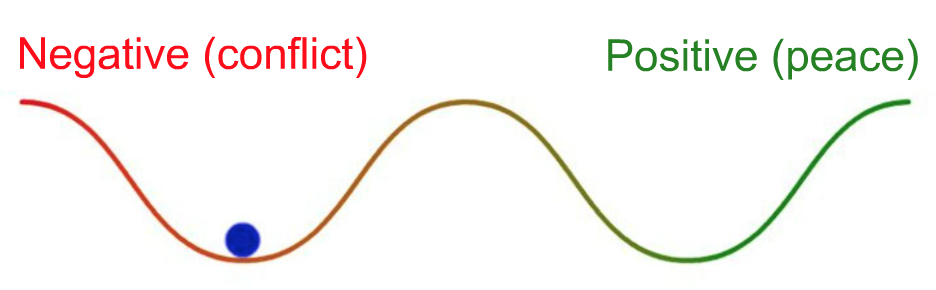 rauhantutkimus: rauha ei ole pelkkää sodan puuttumista – ne ovat erilaisia attraktoreita!
(lähde)
rauhantutkimus: rauha ei ole pelkkää sodan puuttumista – ne ovat erilaisia attraktoreita!
(lähde)
Katsotaan vielä lopuksi kalastussimulaatiomme, kaikki osat yhdessä:
Kun seuraavan kerran ihmettelet, miksi asiat ovat jotenkin jumissa, mieti seuraavaa:
- Mitkä ovat järjestelmän “attraktorit”?
- Kuinka "syviä" laaksot ovat? (syvempi = vaikeampi paeta)
- Kuinka "leveitä" laaksot ovat? (leveämpi = suurempi vetovoima-alue)
- Voimmeko pelkän pallon liikuttamisen sijaan siirtää kukkuloita? (taustalla olevan järjestelmän muuttaminen)
Ja jos koskaan huomaat olevasi turhautunut maailmaan, muista: monissa järjestelmissä mikään ei muutu pitkään aikaan.
Sitten kaikki muuttuu.