Некое мирное движение годами борется с насилием и угнетением, и ничего особо не меняется. Но затем, меняется всё.
Почему многие сложные системы – культуры, природные среды, экономики – находятся в застрявшем состоянии (или же, если к лучшему, в "стабильном" состоянии) вопреки многим усилиям их изменить? И почему, когда изменения всё-таки происходят, они вызывают каскад (или же, если к худшему, "коллапс") всего и сразу?
Существует инструмент, который может помочь нам это понять:
аттракторные рельефы ![]() (от англ. "attract" - "притягивать").
Или, говоря простым языком: "мячик, катающийся по горкам".
Изначально этот инструмент был создан в области физики,
но с тех пор использовался, чтобы помочь нам понять генетику, неврологию, политику, и не только!
(от англ. "attract" - "притягивать").
Или, говоря простым языком: "мячик, катающийся по горкам".
Изначально этот инструмент был создан в области физики,
но с тех пор использовался, чтобы помочь нам понять генетику, неврологию, политику, и не только!
Я объясню, что такое аттракторы (точки притяжения) с помощью примера из экологии. Представим, что вы рыбачите на маленьком отстойном пруду. Вы можете израсходовать ваш природный ресурс (рыбу) довольно быстро...
нажимайте на кнопки и двигайте ползунки:
К счастью, рыба размножается, так что численность ваших рыбок со временем возрастёт обратно. К НЕсчастью, превысив определённый порог, рыбки умирают от перенаселения. И к двойному несчастью, опустившись ниже определённого порога, рыбки не будут успевать размножаться быстрее, чем они умирают.
Ну а теперь, давайте пойдём на рыбалку, учитывая эти могучие силы жизни и смерти:
Если не ловить слишком много рыбы, экосистема всегда остаётся "притянутой" к численности=70. Вполне устойчиво! Однако, поймайте слишком много, и экосистема "притянется" к численности=0. Вы погубили их всех!
Ничего особо не меняется. Затем, меняется всё.
Именно поэтому численность=0 и численность=70 называют аттракторами (точками притяжения): потому что они "притягивают" систему к себе. Подобным образом численность=30 называется репеллером (точкой отталкивания, от англ. "repel" - "отталкивать"), потому что если численность будет хоть немного больше или меньше 30, то она будет "отталкиваться" от этой 30. Численность=30 также называют критической точкой или точкой перехода, так как именно здесь экосистема "переходит" с аттрактора 'численность=70' к аттрактору 'численность=0'.
Ойой, как-то много слов.
А не было бы здорово просто увидеть как ведёт себя система на всех возможных значениях численности?
Вот тут-то и приходят на помощь аттракторные рельефы!
Если мы преобразуем темп рождаемости/смертности ![]() в несколько горных склонов
в несколько горных склонов ![]() (быстрее темп → круче склон) и поместим на верх мячик
(быстрее темп → круче склон) и поместим на верх мячик ![]() ,
то получим что-то вроде этого:
,
то получим что-то вроде этого:
Теперь, изобразив систему как рельеф, мы можем понять её работу гораздо легче!
Возвышенности ![]() - это репеллеры;
низменности
- это репеллеры;
низменности ![]() - аттракторы.
- аттракторы.
Глубина низменности показывает силу, необходимую для "отрыва" от аттрактора. (напр.: глубина численности=0 больше, чем у численности=70; именно поэтому обрушить экосистему проще, чем её восстановить)
Ширина низменности называется чашей притяжения. Она показывает диапазон, в котором аттрактор делает свою... "работу". (напр.: чашей притяжения численности=70 является любое значение в пределах 30<численность≤100)
(Примечание: наш аттракторный рельеф двухмерный, ведь мы берём всего один параметр: численность. Будь у нас больше параметров, мы могли бы создать трёхмерный рельеф, или даже четырёх-, пяти-, да хоть СТОмерный рельеф! При большем кол-ве измерений мы даже можем получить нечто, именуемое странными аттракторами... но об этом как-нибудь в другой раз.)
Переводя на нашу метафору "мячик-горка", ловля и освобождение рыбы это наши попытки подвинуть мячик. Но что будет, если мы сможем сдвинуть горки? В нашем рыбном примере это значит изменение аттракторов экосистемы путем повторного введения хищников, увеличения растительной жизни и т.д.
Если двигать только мячик, то он, скорее всего, просто вернётся к аттрактору. Но если сдвинуть горки, то изменения сохранятся! А всё потому, что вы фундаментально меняете систему.
Рассмотрим парочку нерыбных примеров чтобы показать, каким могущественным инструментом для понимания работы систем являются аттракторные рельефы. Вот несколько из настоящих академических документов (по их виду можно понять, что они академические, их как-будто в паверпоинте сделали):
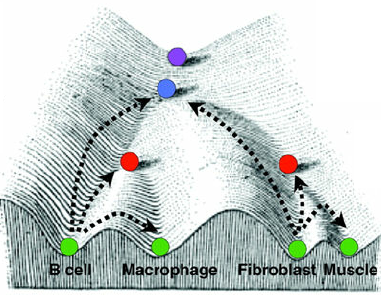 эпигенетика: как стволовые клетки становятся специализированными клетками.
(источник)
эпигенетика: как стволовые клетки становятся специализированными клетками.
(источник)
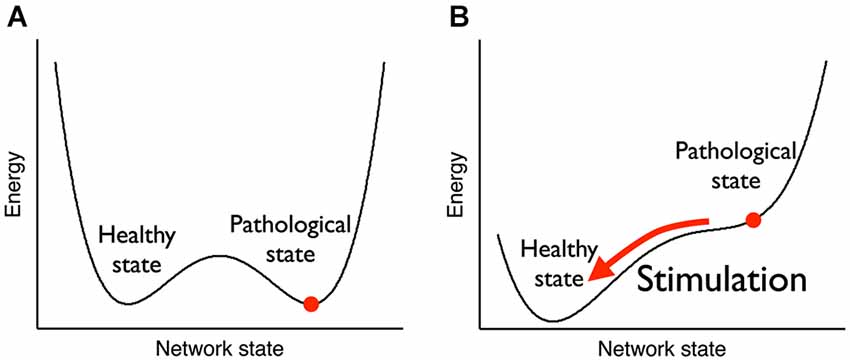 неврология: неврологическая стимуляция выводит мозг из стабильного нездорового состояния к стабильноиу здоровому.
(источник)
неврология: неврологическая стимуляция выводит мозг из стабильного нездорового состояния к стабильноиу здоровому.
(источник)
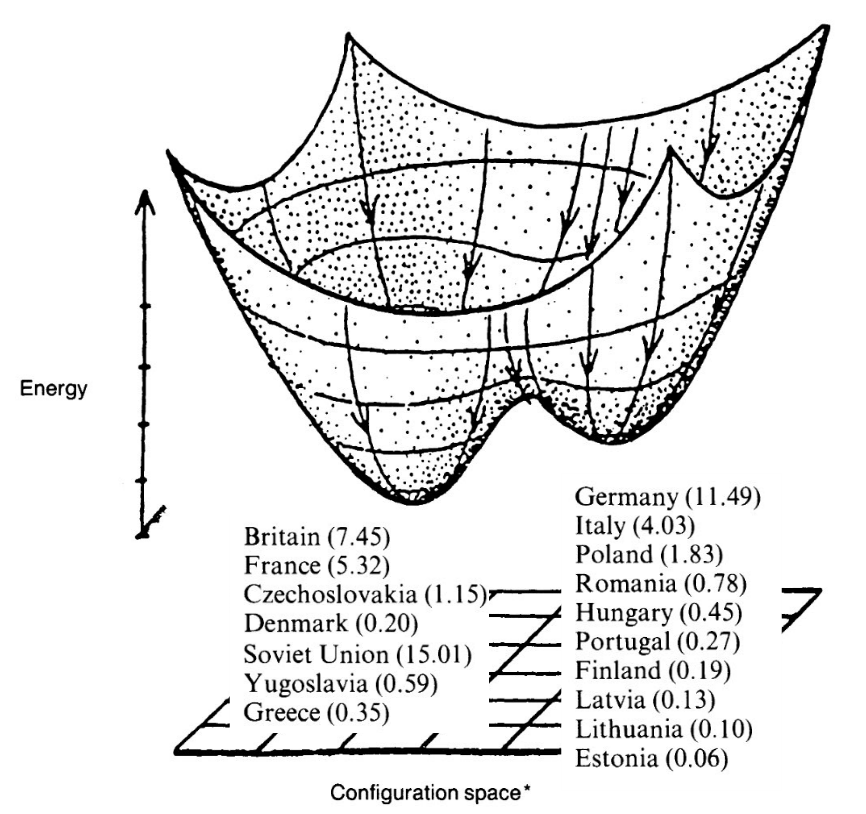 политика: "прогноз" вероятных политических связей во время Второй мировой войны.
(источник)
политика: "прогноз" вероятных политических связей во время Второй мировой войны.
(источник)
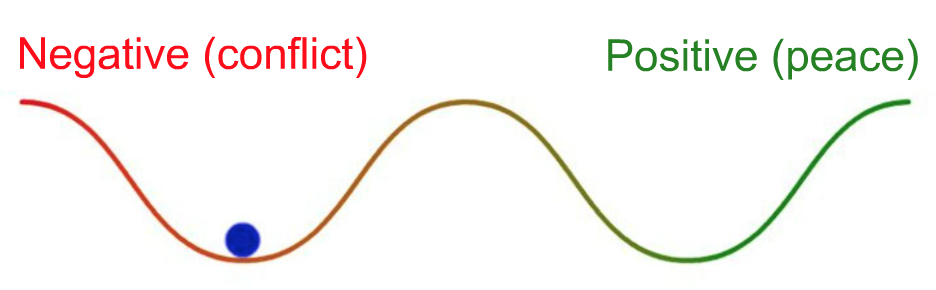 исследования мира: мир - это не просто отсутствие войны, они - два разных аттрактора!
(источник)
исследования мира: мир - это не просто отсутствие войны, они - два разных аттрактора!
(источник)
И наконец, посмотрим ещё разок на наш симулятор рыбалки, учитывая всё-всё!
Итак, теперь, когда вы в следующий раз задумаетесь, почему что-то "зависает" в каком-то месте, подумайте:
- Какие у этой системы "аттракторы"?
- Насколько "глубокие" низменности системы? (чем глубже - тем сложнее вырваться)
- Насколько "широкие" эти низменности? (чем шире - тем больше радиус действия)
- Можно ли подвинуть не только мячик, но и горки? (изменить систему фундаментально)
И если вы ещё когда-нибудь почуствуете себя разочарованными всем миром, помните: для множества систем, долгое время ничего особо не меняется.
Но затем, меняется всё.